Table des matières

LA RÉSISTANCE ÉLECTRIQUE

LA RÉSISTANCE ÉLECTRIQUE

Comprendre ce qu'est une résistance électrique

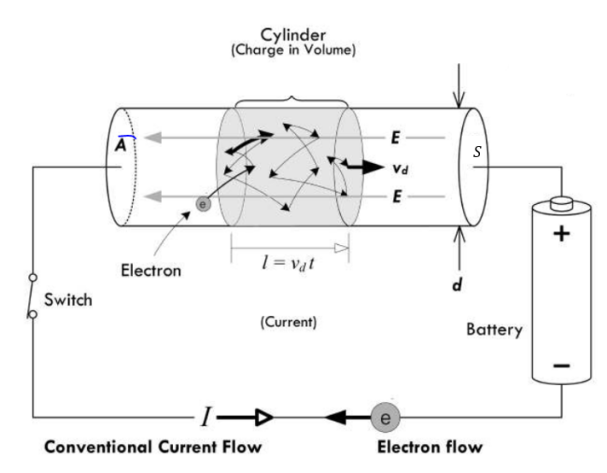
Prenons un conducteur, alimenté par une pile. Cette pile impose une différence de potentiel électrique entre les deux extrémités.

Le conducteur est de section S et de longueur L. Les électrons libres sont accélérés par le champ électrique E.

En effet la force électrostatique vaut $F = q \cdot E$ .

D'après la seconde loi de Newton $F = m \cdot a$ .

Dans le vide un électron libre serait accéléré à $a= \frac{e}{m} \cdot E$

La vitesse pourrait devenir infinie. C'est ce principe qui est utilisé dans les accélérateurs de particules sur les portions droites.

Dans la réalité nos électrons libres vont heurter les atomes et donc être fréquemment ralentis puis être accélérés par le champ électrique E.

Si l'on considère la force de frottement on peut écrire que $F_f = -k'\cdot v_d$

La seconde loi de Newton permet d'écrire $F_e-F_f = m\cdot a$ .

L'accélération s'annule quand $F_e-F_f = 0$ soit $F_e=F_f$ ou $q \cdot E = k'\cdot v_d$

La vitesse limite sera donc $v_d = \frac{q}{k'} \cdot E$

Ainsi la vitesse de dérive globale des électrons vaudra $v_d = \frac{q}{k'} \cdot E = \mu \cdot E$ .

Considérons la charge contenue dans le volume $\Delta V = S\cdot l = S\cdot v_d\cdot t$

La charge contenue dans ce volume vaut: $~\Delta Q = n \cdot e \cdot \Delta V$ (avec n la densité volumique de charges)

soit $~\Delta Q = n \cdot e \cdot S\cdot v_d\cdot \Delta t$

ou $~\Delta Q = n \cdot e \cdot S\cdot \mu \cdot E \cdot \Delta t$

Par définition $I = {{\Delta Q} \over {\Delta t}}$

$~I = \mu \cdot n\cdot e\cdot S \cdot {{U} \over {L}}$

Posons $\rho = \frac{1}{\mu \cdot n\cdot e}$

Cela donne $I = \frac{1}{\rho} \cdot S \cdot {{U} \over {L}}$

ou $R = \frac{U}{I} = \rho \cdot {{L} \over {S}}$ c'est la loi d'ohm.

Fondamental

Ainsi la résistance électrique est liée à la vitesse de dérive des électrons dans le conducteur. Si cette vitesse est faible, $\mu$ est faible et la résistance est élevée.

Plus le fil est long, plus les collisions se multiplient, ce qui ralentit les électrons et augmente la résistance.

Augmenter la section du fil permet de mieux écouler le courant électrique, ce qui diminue la résistance électrique.

Remarque

Levons une idée qui est souvent confuse dans l'esprit de beaucoup. Ce ne sont pas les électrons eux-mêmes qui transportent l'énergie électrique ! Calculons la vitesse de dérive pour un courant de un ampère dans un conducteur de 2.5 mm².

Calculons la vitesse de dérive vd des électrons dans un fil de cuivre de section 2,5 mm² parcouru par un courant de 1 A.

Formule de la vitesse de dérive : $v_d = \rho \cdot I = \frac{I}{n \cdot e \cdot S}$

où :

I=1A : courant.

$n=8,5 \cdot 10^{28} ~électrons~ \cdot m^{-3}$ : densité d’électrons libres (nombre d’électrons libres par m³), ce qui est très élevé !.

$e=1,602 \cdot 10^{-19} ~C$ : charge élémentaire.

$S=2,5 \cdot 10^{-6}~ m^2$ : section du conducteur.

Calcul de la vitesse de dérive $v_d \simeq 2,94 \cdot 10^{-5} ~m \cdot s^{-1}$ .

Cette vitesse est très faible ! La vitesse de dérive des électrons dans un conducteur est généralement très lente, de l'ordre de quelques millimètres par seconde, voire quelques centimètres par heure dans un fil de cuivre. Cependant, le champ électrique se propage très rapidement, presque à la vitesse de la lumière, ce qui explique pourquoi les circuits réagissent presque instantanément aux changements. Cette distinction est importante car la vitesse de dérive fait référence au mouvement des électrons eux-mêmes, tandis que la vitesse de propagation du champ électrique est liée à la transmission des signaux électromagnétiques. En d'autres termes, les électrons se déplacent lentement, mais le signal électrique, qui est transmis par le champ électrique, se propage très rapidement. Cette différence peut être illustrée par l'analogie d'un tuyau d'arrosage déjà plein d'eau : lorsque le robinet est ouvert, l'eau sort immédiatement de l'autre extrémité, même si les molécules d'eau ne se déplacent que lentement.

Fondamental

Alors d’où vient l’énergie ?

L’énergie circule dans le champ électromagnétique créé par la combinaison du :

Champ électrique (produit par la pile ou le générateur),

Champ magnétique (produit par le courant lui-même).

L’énergie n’est pas contenue dans les électrons, mais dans les champs qui se forment autour du fil, et qui propulsent l’énergie jusqu’aux appareils (lampe, moteur…).

Un exemple d'ingénierie défaillante

Le câble transatlantique de 1858 : un échec instructif.

Contexte :

Premier câble sous-marin transatlantique installé entre l’Irlande et Terre-Neuve (env. 4000 km).

Objectif : transmettre des messages télégraphiques entre l’Europe et l’Amérique.

Inauguré en août 1858, il fonctionna quelques semaines seulement.

Problèmes rencontrés :

Signal très faible à l’arrivée :

Le courant envoyé à une extrémité mettait des secondes à produire un effet à l’autre bout.

Cela était dû à une forte capacitance du câble (le cuivre était entouré de gutta-percha, un isolant naturel).

Ce système se comportait comme une ligne de transmission avec effet capacitif et inductif, mais les ingénieurs de l’époque n’avaient pas encore ce modèle en tête.

Tentative de “forcer le signal” :

Pour compenser la faiblesse, les opérateurs ont augmenté la tension, espérant un meilleur signal.

Cela a endommagé l’isolation du câble — le câble a grillé intérieurement.

Mauvaise compréhension du rôle du champ électromagnétique :

À l’époque, les ingénieurs pensaient encore le courant comme un flux de fluide.

Ils n’avaient pas encore pleinement intégré les notions de vitesse de propagation du signal, réflexion, impédance, etc..

James Clerk Maxwell n’avait pas encore publié ses équations définitives.

Ce qu’on comprend aujourd’hui (et que l’on ignorait alors) :

Dans un câble long, le courant ne s’installe pas instantanément.

Le signal électrique se propage à travers les champs électromagnétiques autour du câble, pas “dans” le cuivre.

Le câble agit comme une ligne de transmission :

Il a une capacité (entre le conducteur et l’eau autour),

Une inductance (à cause du champ magnétique produit par le courant),

Et une résistance du conducteur.

Pour éviter les réflexions et pertes, on doit adapter l’impédance et limiter la bande passante.

Leçon importante :

Le mauvais fonctionnement du câble ne venait ni du cuivre, ni des électrons, mais d’une mauvaise compréhension du champ électromagnétique et de la physique de la transmission du signal.

Association de résistances

Résistances en série

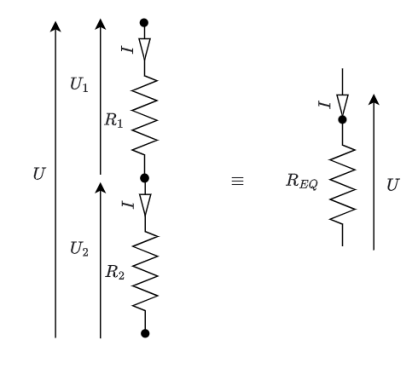
Deux résistances sont placées en série. Par quelle résistance faut-il les remplacer pour obtenir une résistance équivalente ?

La loi d'ohm sur $R_1$ permet d'écrire : $U_1 = R_1 \cdot I$ .

La loi d'ohm sur $R_2$ permet d'écrire : $U_2 = R_2 \cdot I$ .

La loi d'ohm sur $R_{EQ}$ permet d'écrire : $U = R_{EQ} \cdot I$ .

On remarque également que $U = U_1+ U_2$ soit $U = R_1 \cdot I + R_2 \cdot I = (R_1 + R_2) \cdot I$ .

$\left\{ \begin{aligned} U &= R_{EQ} \cdot I \\ U &= (R_1 + R_2) \cdot I \end{aligned} \right.$

Conclusion $\boxed{R_{EQ}=R_1 + R_2}$

Définition

La résistance équivalente à plusieurs résistances en série vaut la somme de ces résistances.

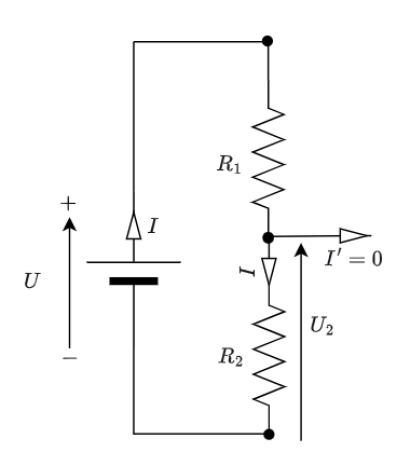
Dans ce contexte on doit parler du pont diviseur de tension qui est un circuit constitué d 'au moins deux résistances en série.

Quelle est la relation entre $U,~U_2,~R_1~et~R_2$ ?

La loi d'ohm sur $R_2$ permet d'écrire : $~U_2 = R_2 \cdot I$ .

La loi d'ohm sur $R_{EQ}$ permet d'écrire : $~U = R_{EQ} \cdot I = (R_{1} + R{2}) \cdot I$ .

$~I = {\frac {U}{R_1+R_2}}$

On déduit que : $~ U_2 = R_2 \cdot {\frac {U}{R_1+R_2}}$ soit $~ \boxed{U_2 =U\cdot {\frac {R_2}{R_1+R_2}}}$

Résistances en dérivation

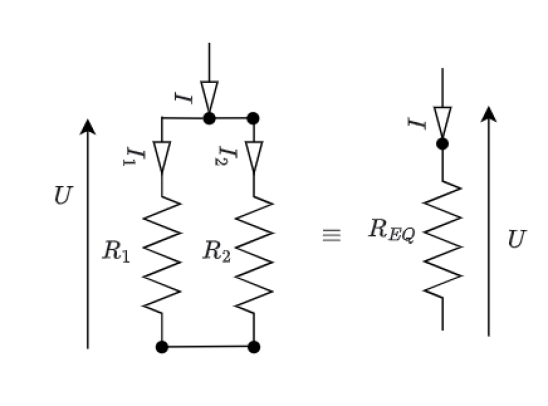
Deux résistances sont placées en dérivation. Par quelle résistance faut-il les remplacer pour obtenir une résistance équivalente ?

La loi des nœuds permet d'écrire : $I = I_1+ I_2$

La loi d'ohm sur R_1 permet d'écrire : $I_1 = U \div R_1$ .

La loi d'ohm sur R_2 permet d'écrire : $I_2 = U \div R_2$ .

La loi d'ohm sur R_{EQ} permet d'écrire : $I = U \div R_{EQ}$ .

$\boxed{\frac{1}{R_{EQ}} = \frac{1}{R_{1}} +\frac{1}{R_{2}}}$

Conclusion

$\boxed{R_{EQ}=\frac{R_1 \cdot R_2}{R_1+R_2}}$

Définition

L'inverse de la résistance équivalente à plusieurs résistances en dérivation vaut la somme de l'inverse de ces résistances.

Remarque

Deux résistances en dérivation se comporte comme un diviseur de courant.

Notons $U = R_1 \cdot I_1 = R_{EQ} \cdot I$ .

Soit $~I_1 = {\frac {R_{EQ}} {R_1}} \cdot I = {\frac {\frac{R_1 \cdot R_2}{R_1+R_2}} {R_1}} \cdot I$

$\boxed{I_1 = {\frac {R_{2}} {R_1+R_2}} \cdot I} ~\boxed{I_2 = {\frac {R_{1}} {R_1+R_2}} \cdot I}$

En posons $G_1 = 1 \div R_1 ~et~ G_2 = 1 \div R_2$ on arrive à $\boxed{I_1 = {\frac {G_{1}} {G_1+G_2}} \cdot I} ~\boxed{I_2 = {\frac {G_{2}} {G_1+G_2}} \cdot I}$

Synthèse

Résumons nous :

Le courant électrique est un débit d'électrons. On note $~I = {\Delta Q \over \Delta t }$ .

La tension électrique est comparable à une pression électrique engendrée par un générateur de tension qui agit comme une pompe à électrons. Comme ce générateur impose des concentrations de charges différentes, il impose une différence de potentiel électrique. Ce qui engendre un champ électrique E.

La force électrostatique a pour expression $~F = k \cdot {{q_1 \cdot q_2} \over {d^2}}$

Si on note $~E = k \cdot {{q_2} \over {d^2}}$ il vient que $~F = q_1 \cdot E$

Le travail de cette force sur une distance L vaudra $W(F) = F \cdot L = q_1 \cdot E \cdot L = q_1 \cdot U$ car $U = E \cdot L$ si on considère E uniforme et L aligné sur la direction du champ.

La tension électrique peut donc être vue comme l'énergie nécessaire pour déplacer 1 coulomb de charge. En mécanique quantique on utilise comme unité d'énergie l'électron-volt (eV).

Comme $~q_1= I \cdot t ~$ on peut noter $~W(F) =U \cdot q_1$ ou $~W(F) =U \cdot I \cdot t$ .

Comme la puissance électrique est le quotient de l'énergie par le temps on peut écrire $P_{élec} = U\cdot I$ . La puissance est toujours le produit d'une grandeur effort par un grandeur flux.

La résistance électrique provient des multiples collisions des élections libres au sein du matériau. Ces collisions échauffent le matériau. Sa valeur selon la loi géométrique vaut $~R = {{\rho \cdot L} \over S}$ .

La loi d'ohm précise que $U = R \cdot I$ .

Il y a beaucoup d'électrons libres dans un conducteur et la vitesse de dérive des électrons est très faible (quelques millimètres par secondes). Ce ne sont donc pas les électrons eux-mêmes qui transmettent la puissance électrique mais la transmission d'un champ électro-magnétique qui se déplace à deux tiers de la vitesse de la lumière. En résumé : les électrons se déplacent lentement, mais l'énergie, elle, voyage vite — portée non par la matière, mais par les champs qui l'entourent.

A quoi sert une résistance électrique ?

La résistance électrique est la base de l'électricité et de l'électronique. Le but de cette partie est de montrer la variété des applications et le comportement réel d'une résistance.

La famille des résistances électrique est une grande famille. Pourquoi une telle diversité ? La loi d(ohm est leur fondement. $U = R \cdot I$ . Mais également l loi de joule. $P = R \cdot I^2$ . La résistance évolue en fonction de la température selon un coefficient thermique nommé $\alpha$ . La loi est la suivante : $R(T)=R_0 \cdot (1 + \alpha \cdot (T-T_0))$ .Une résistance faible aura tendance à chauffer. C'est un effet parfois recherché.

Une résistance de faible valeur traversée par un fort courant peut chauffer fortement : c’est parfois un effet désiré (résistance chauffante ou fusible), parfois dangereux (surchauffe, destruction).

Exemple1 : Le cas classique de l'utilisation d'une résistance est de créer une chute de tension pour adapter la tension et limiter ainsi le courant délivré. Le cas le plus typique et celui de la diode DEL. La diode a un courant qui devient exponentiel lorsque la tension augmente. On risque donc de détruire le composant. Il faut donc ajouter une résistance à la DEL pour la protéger.

La figure ci-dessus représente le circuit avec la DEL et sa résistance de protection. On notera la droite en rouge qui correspond à la droite de charge. L'intersection de cette droite de charge avec la caractéristique de la DEL donne le point de fonctionnement. Pratiquement nous choisissons une intensité de 10mA et nous faisons remonter l droite de charge de (5V,0 mA) au point (2.7V, 10 mA).

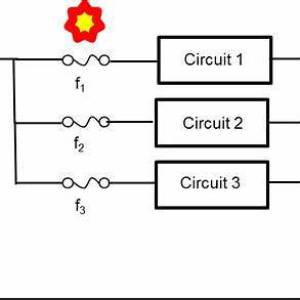
Exemple2 : Un fusible peut-être vu comme une résistance de faible valeur paramétrée pour fondre à partir d'une certaine intensité. C’est un dispositif de sécurité

Exemple3 : Dans un sèche-linge, lave-vaisselle ou machine à laver, on trouve une résistance chauffante (souvent bobinée), utilisée pour transformer l’énergie électrique en chaleur (effet Joule).

Attention

De ce qui précède il conviendra pour une résistance non seulement de déterminer sa valeur mais également de déterminer sa capacité de transmission de puissance. Plus la résistance est volumineuse, plus elle est capable de dissiper une forte puissance.

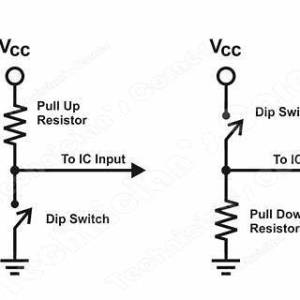
Exemple4 : La résistance de tirage (pull-up ou pull-down) permet pour une entrée de microcontrôleur de ne pas laisser l'entrée sans référence de tension. Dans ce cas elle se comporterai comme une antenne et produirait des signaux aléatoires. La résistance de tirage évite ce comportement.

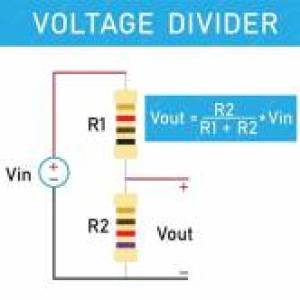
Exemple5 : Le pont diviseur est souvent utilisé pour produire une tension de sortie à partir d'une tension d'entrée.

Attention

Pour le pont diviseur il faut s'assurer qu'aucun courant (ou à tout le moins un courant négligeable) ne circule sur le potentiel positif de la tension de sortie, sans quoi la loi donnée ci-dessus se révèle fausse. La charge doit donc avoir une résistance élevée.

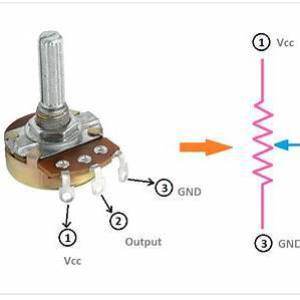
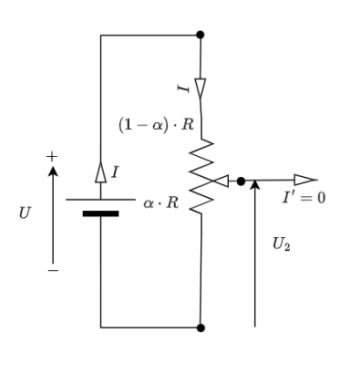
Prenons un potentiomètre et essayant de faire varier la tension transmise à un moteur.

Le pont diviseur devient :

$\alpha$ représente ici la proportion de la résistance totale exposée à la sortie. Il évolue entre 0 (tout en bas) et 1 (tout en haut). On trouve $V_s = \alpha \cdot U$ . Si vous branchez un moteur sur ce potentiomètre, cela ne marchera pas. Pourquoi ? Parce que le moteur à une résistance d'induit de quelques ohms. Il consommera donc un courant non négligeable. Si le moteur a une faible résistance (ex : 5 Ω), il consomme un courant important → le pont diviseur est perturbé.Nous verrons ultérieurement l'utilité d'un hacheur série utilisant la MLI ou la PWM comme on dit outre-manche.

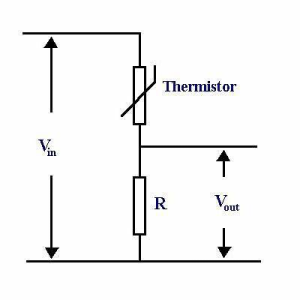
Le pont diviseur de tension est souvent utilisé avec un capteur dans la résistance électrique varie avec l'évolution d'une grandeur physique. On associe alors :

une résistance fixe,
et une résistance variable, dépendant de la grandeur mesurée :
- CTN (température),
- LDR (lumière),
- jauge de contrainte (déformation mécanique).

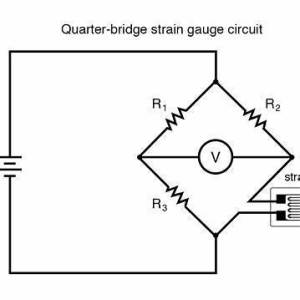
La dernière figure représente un pont de Wheatstone. Il est en fait formé de deux pont diviseurs de tensions accolés. La jauge de contrainte subit des déformations mécaniques et donc des variations de longueur. Ces variations de longueur se traduisent par des variations de résistance électrique. La tension mesurée sur le pont est directement proportionnelle à l'effort exercé sur la jauge de contrainte.