Table des matières

LES LOIS ÉLECTRIQUES

LES LOIS ÉLECTRIQUES

Les schémas électriques

Comment représenter ce qu'il se passe dans les atomes ? Comment représenter une tension ? Un courant ? Une résistance ? Des conventions ont été adoptées et des normes existent pour représenter les circuits électriques ou électroniques.

En génie électrique, nous nous intéressons à communiquer ou de transférer l’énergie d’un point à un autre. Pour ce faire, nous interconnectons des appareils électriques. Cette interconnexion est appelé circuit électrique et chaque composant du circuit est appelé élément du circuit électrique. .

Tout circuit est constitué :

D'un générateur de tension (continu ou alternatif)
D'un actionneur qui transforme l'énergie électrique (lampe, résistance chauffante …)
De fils pour interconnecter le tout
De composants divers et variés (résistances, bobinages , condensateurs, diodes, transistors, etc …)

Le but de ce câblage est d'assurer des exigences fonctionnelles attendues par le client. Pour bien répondre à la demande des clients l'ingénieur (ou l'ingénieure !), le technicien (la technicienne !), doivent maîtriser les divers composants leur intérêt, leur limite, leurs qualités, leur défauts.

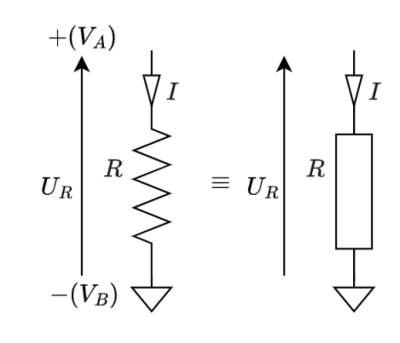
Ci-dessus est représenté une résistance à la norme européenne IEEE. Pour indiquer une tension on place généralement un flêche partant du potentiel le plus bas (-) au potentiel le plus haut (+).

$U =V_a - V_b$ est un tension électrique, donc une différence de potentiel électrique. Le potentiel se trouve en un seul point, mais la tension se trouve entre deux potentiels.

Une pile ou un accumulateur peut se représenter de cette manière. Dans un récepteur, le courant I lui se déplacera du potentiel le plus haut vers le potentiel le plus bas. Par contre dans un générateur comme une pile le courant le courant I lui se déplacera du potentiel le plus bas vers le potentiel le plus haut car c'est justement le rôle du générateur d'accélérer les électrons dans le conducteur.

Rappelons que la tension est par définition l'énergie nécessaire pour déplacer 1 coulomb de charges soit $U = {{dW} \over {dQ}}$ .

Nous pouvons ici écrire la loi d'ohm qui précise que $U_R = R \cdot I$ ou les variantes $R = {{U_R} \over I}$ et $I ={ {U_R} \over R}$ .

Pour la puissance dissipée dans cette résistance $U = {{dW} \over {dQ}}$ en multipliant par $I = {{dQ} \over {dt}}$ on obtient $P = U \cdot I = {{dW} \over {dQ}} \cdot {{dQ} \over {dt}} = {{dW} \over {dt}}$

Exercice résolu

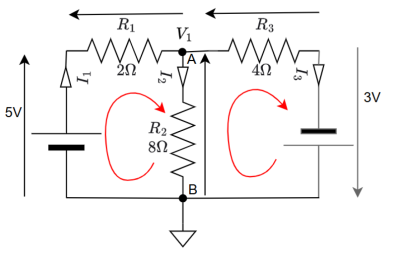
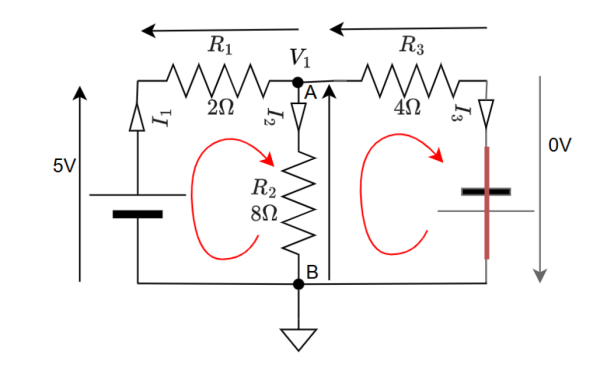
Le circuit ci-dessus est constitué de deux nœuds (A et B). Au nœud A la quantité de charges doit rester constante.

Ainsi l'équation du nœud A s'écrira: $-I_1 -I_2 -I_3 = 0$ . Pourquoi? Parce que chaque courant qui quitte le nœud est négatif, s'il entre dans le nœud il est positif.

L'équation du nœud B s'écrira: $~ I_1 + I_2 + I_3 = 0$ .

On remarque que le nœud B est symétrique par rapport au nœud A.

Il nous faut rajouter la loi d'ohm pour les trois résistances. Ainsi le système d'équations devient :

$~ I_1 + I_2 + I_3 = 0$

$V_1 - 5 = 2 \cdot I_1$

$V_1 = 8 \cdot I_2$

$V_1 - -3 = 4\cdot I_3$

Nous avons quatre inconnues et quatre équations. En substituant les intensités dans la loi des noeuds on obtient:

${{V_1 - 5} \over 2 } +{{V_1} \over 8}+{{V_1 +3} \over 4} = 0$

et ${{V_1} \over 2 } +{{V_1} \over 8}+{{V_1} \over 4} = {{5} \over 2 } - {{3} \over 4}$

donc ${{4 \cdot V_1} \over 8} +{{ V_1} \over 8}+{{2 \cdot V_1} \over 8} = {{10} \over 4} - {{3} \over 4} et {{7 \cdot V_1} \over 8} = {{7} \over 4} = {{14} \over 8}$

ainsi $V_1 = 2 ~volts$ .

Calculons les intensités des courants : $I_1 = {{2-5} \over 2} ={{-3} \over 2} A ={{-12} \over 8} A$ .

$I_2 = {{2} \over 8} A$ .

$I_3 = {{2--3} \over 4} ={{5} \over 4} A = {{10} \over 8} A$ .

On retrouve bien $~ I_1 + I_2 + I_3 = 0$ mais $~ I_1$ est négatif, ce qui signifie que l'on s'est trompé de sens ! En effet $~I_1$ est le courant du générateur , il devrait donc être dans le même sens que la tension du générateur car il est fourni par ce dernier.

Les lois de Kirchhoff

Les lois de Kirchhoff Trouver le nombre de nœuds, c'est identifier dans le circuit les équipotentielles, c'est à dire tous les points qui partagent la même tension. Ce repérage laisse apparaître des branches. Une maille sera définie comme une succession de branches formant un circuit fermé (cf boucle 1 et boucle 2).

Les lois de Kirchhoff stipulent que :

La somme des courants entrant par un nœud est égale à la somme des courants sortant par le même nœud. (Conservation de la charge électrique).
La loi des tensions de Kirchhoff stipule que la somme algébrique des tensions le long d’une maille est constamment nulle. Les tensions rencontrées lors du parcours de la maille sont positives si elles s'alignent sur ce parcours et négatives si elles s'y opposent. (Conservation de l'énergie).

Cette dernière provient du fait que le parcours d'un champ électrique sur un circuit fermé signifie que la tension est nulle. En effet $U = E \cdot L = V_a - V_b$ . Si la longueur du parcours est nulle (circuit fermé : le point A correspond au point B) la différence de potentiel (et donc la tension) est nul.

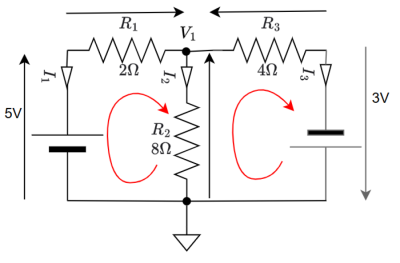
Reprenons notre exemple avec le courant $~ I_1$ correctement positionné.

L'application des lois de Kirchhoff donne :

nœud A : $I_1 - I_2 - I_3 = 0$

boucle 1 : $5 - V_{2\Omega} - V_1= 0$

boucle2 : $V_1 - V_{4\Omega} +3= 0$

L'application de la loi d'ohm donne :

$2\Omega : V_{2\Omega} = 2 \cdot I_1$

$8\Omega : V_1 = 8 \cdot I_2$

$4\Omega : V_{4\Omega} = 4 \cdot I_3$

Le système devient :

nœud A : $I_1 - I_2 - I_3 = 0 \text~(1)$

boucle 1 : $5 - 2 \cdot I_1- 8 \cdot I_2= 0 \text~(2)$

boucle2 : $8 \cdot I_2 - 4 \cdot I_3+3= 0 \text~(3)$

Méthode de résolution par substitution

Étape 1 : Isoler $I_1$ dans l’équation (1)

$I_1 = I_2 + I_3 \quad \text{(Éq. 1')}$

Étape 2 : Remplacer $I_1$ dans l’équation (2)

$\begin{aligned} 5 - 2 \cdot (I_2 + I_3) - 8 \cdot I_2 &= 0 \\ 5 - 2 \cdot I_2 - 2 \cdot I_3 - 8 \cdot I_2 &= 0 \\ 5 - 10 \cdot I_2 - 2 \cdot I_3 &= 0 \\ \Rightarrow 10 \cdot I_2 + 2 \cdot I_3 &= 5 \quad \text{(Éq. 2')} \end{aligned}$

Étape 3 : Simplifier l’équation (2')

$5 \cdot I_2 + I_3 = 2.5 \quad \text{(Éq. 4)}$

Étape 4 : Simplifier l’équation (3)

$\begin{aligned} 8 \cdot I_2 - 4 \cdot I_3 + 3 &= 0 \\ \Rightarrow 8 \cdot I_2 - 4 \cdot I_3 &= -3 \quad \text{(Éq. 5)} \end{aligned}$

Étape 5 : Résoudre le système formé par les équations (4) et (5)

$\begin{aligned} \text{Éq. (4) : } 5 \cdot I_2 + I_3 &= 2.5 \\ \Rightarrow I_3 &= 2.5 - 5 \cdot I_2 \quad \text{(Éq. 6)} \end{aligned}$

Remplacer dans Éq. (5) :

$\begin{aligned} 8 \cdot I_2 - 4(2.5 - 5 \cdot I_2) &= -3 \\ 8 \cdot I_2 - 10 + 20 \cdot I_2 &= -3 \\ 28 \cdot I_2 - 10 &= -3 \\ 28 \cdot I_2 &= 7 \\ I_2 &= \frac{1}{4} \text{ A} \end{aligned}$

Étape 6 : Trouver $I_3$

Avec $Éq. (6)$ : $I_3 = 2.5 - 5 \cdot \frac{1}{4} = 2.5 - 1.25 = 1.25 \text{ A}$

Étape 7 : Trouver $I_1$

Avec $Éq. (1') :I_1 = I_2 + I_3 = \frac{1}{4} + \frac{5}{4} = \frac{6}{4} = 1.5 \text{ A}$

Résultats finaux :

$\boxed{I_1 = 1.5\ \text{A},\quad I_2 = 0.25\ \text{A},\quad I_3 = 1.25\ \text{A}} ~Comme~ V_1 = 8 \cdot I_2 ~\boxed{V_1 = 2~Volts}$

Les théorèmes de Thevenin et Norton

Le théorème de Thévenin permet de simplifier un circuit électrique par l'équivalence d'une source de tension $E_{TH}$ et d'une résistance série $R_{TH}$ .

On débranche la «charge» et on calcule le tension obtenue en sortie que l'on nomme $E_{TH}$ .

On neutralise l'alimentation par un court-circuit et on calcule la résistance équivalente nommée $R_{TH}$ .

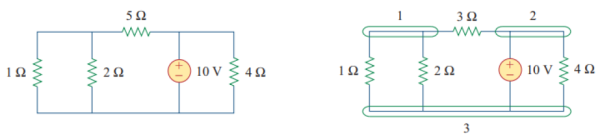
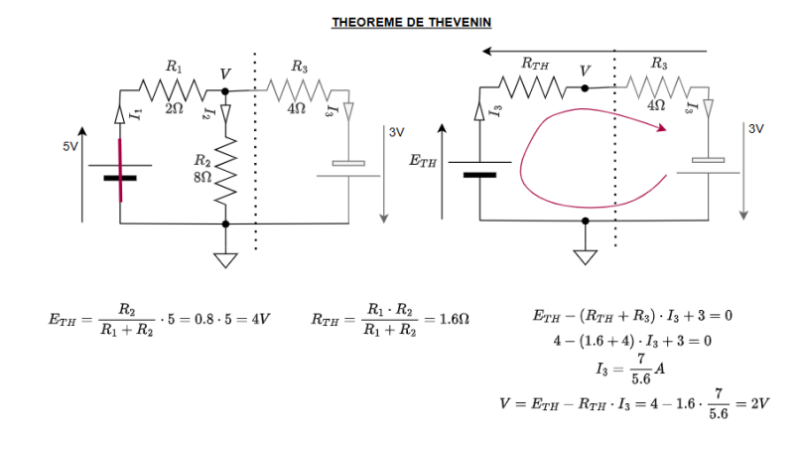
Ci-dessous l'exercice précédent en utilisant le théorème de Thevenin. La charge se situe à droite du trait pointillé.

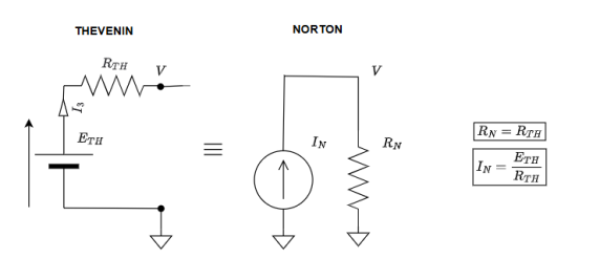
Le modèle de Norton suit la même logique mais remplace le circuit par une source de courant. On neutralise les source de courant en ouvrant le circuit. Ci-dessous l'équivalence entre le modèle de Thevenin et le modèle de Norton.

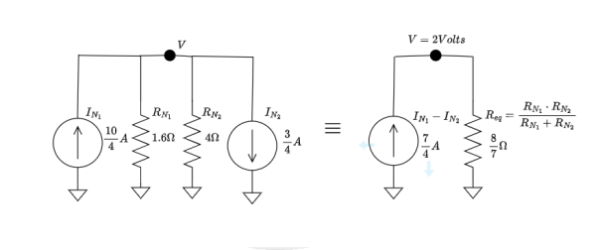
Résolution de l'exercice par application de la méthode de Norton.

Théorème de superposition

Quand un réseau linéaire comporte plusieurs générateurs, l' intensité du courant dans une branche de ce réseau est égale à la somme (algébrique) des intensités des courants créés par chacun des générateurs dans cette branche, les autres générateurs étant remplacés par leur résistance interne ou un court circuit pour un générateur parfait.

On court-circuite le second générateur. Déterminons $I_1', I_2' ~et~ I_3'$ . La résistance de 4 ohms se retrouve en dérivation de la résistance de 8 ohms. La loi d'ohm permet d'écrire :

$V_1 = R_8 \cdot I_2'$

$V_1 = R_4 \cdot I_3'$

Si on considère une résistance équivalente entre A et B, la loi d'ohm permettrait d'écrire $V_1 = R_{AB} \cdot I_1'$ .

La loi des nœuds en A permet d'écrire $I_1' = I_2'+ I_3'$ . Donc $\frac {V_1}{R_{AB}} =\frac {V_1}{R_{8}}+\frac {V_1}{R_{4}} soit \frac {1}{R_{AB}} =\frac {1}{R_{8}}+\frac {1}{R_{4}} \text{ soit } \boxed{R_{AB} = {\frac{R_4 \cdot R_8}{R_4 +R_8}}} \text{ soit } 2.66 ~\Omega$ .

Donc $I_1' = {\frac {5} {2+2.66} } = 1,0714 A$ .

$V_1' = 5 - 2 \cdot 1,0714 = 2.857 V. I_2' = {\frac {2.857} {8} } = 0,357 A \text{ et }I_3' = {\frac {2.857} {4} } = 0,714 A$ .

$\boxed{I_1' = 1.0714\ \text{A},\quad I_2' = 0.357\ \text{A},\quad I_3' = 0.714\ \text{A}}$ .

On court-circuite le premier générateur. Déterminons $I_1", I_2" ~et~ I_3"$ . La résistance de 2 ohms se retrouve en dérivation de la résistance de 8 ohms.

La loi d'ohm permet d'écrire :

$V_1 = R_8 \cdot I_2"$

$V_1 = R_2 \cdot I_3"$

Si on considère une résistance équivalente entre A et B, la loi d'ohm permettrait d'écrire $V_1 = R_{AB} \cdot I_1"$ .

La loi des nœuds en A permet d'écrire $I_1" = I_2"+ I_3"$ . Donc $\frac {V_1}{R_{AB}} =\frac {V_1}{R_{8}}+\frac {V_1}{R_{2}} soit \frac {1}{R_{AB}} =\frac {1}{R_{8}}+\frac {1}{R_{2}} \text{ soit } \boxed{R_{AB} = {\frac{R_2 \cdot R_8}{R_2 +R_8}}} \text{ soit } 1.6 ~\Omega$

Donc $I_3" = {\frac {3} {4+1.6} } = 0,5357 A$ .

$V_1" = -3+ 4 \cdot 0.5357= -0,8571 V\text{. } I_2" = {\frac {0,8571} {8} } = 0,10714 A \text{ et }I_1" = {\frac {0,8571} {2} } = 0,42857 A$ .

$\boxed{I_1" = 0,42857\ \text{A},\quad I_2" = 0,10714\ \text{A},\quad I_3" = 0,5357 A\ \text{A}}$ .

En additionnant la superposition des deux tensions on obtient $V_1 = 2.857 - 0.857 = 2 ~V$ ce qui est cohérent.

Attention : ici le générateur envoie le courant par le bas. L'équation est donc en B. $~ I_3"$ est positif, $~I_1"$ et $~I_2"$ sont négatifs. En $A~I_1"$ et $~I_2"$ sont positifs mais $~I_3"$ est négatif. Finalement $~I_1'$ et $~I_1"$ sont dans le même sens. $~I_3'$ et $~I_3"$ également. Seuls $~I_2'$ et $~I_2"$ s'opposent.

En additionnant la superposition des deux courants on obtient $\boxed{I_1 = 0,42857+1.0714\ \text{A},\quad I_2 = 0.357-0,10714\ \text{A},\quad I_3 = 0,5357+0.714\ \text{A}} . \boxed{I_1 = 1.5\ \text{A},\quad I_2 = 0.25\ \text{A},\quad I_3 = 1.25\ \text{A}}$

Le théorème de Millman

Le théorème de Millman est utile lorsqu'il s'agit de calculer la tension au centre d'une étoile formée de plusieurs brins.

Exemple, le circuit ci-dessous montre comment mixer quatre sources audios différentes :