Table des matières

Découvrir le génie électrique
- Préambule
- Chapitre 1 - Définitions préalables

Découvrir le génie électrique

Préambule

Une chose que j’ai apprise tout au long de la vie :
toute notre science, par rapport à la réalité, est primitive et enfantine.
— Albert Einstein

Prenons le temps de faire un point. Sur une feuille de papier dire :

Ce qu'est le courant électrique,

ce que la tension électrique,

ce qu'est la puissance électrique,

ce qu'est l'énergie électrique,

comment l'énergie se transmet dans un câble électrique,

à quel vitesse se déplace le courant électrique.

Connaissez vous vraiment ce qu'il se passe dans un conducteur électrique ?

Il est fortement recommandé de suivre la vidéo suivante pour pouvoir tester ses représentations et faire le point sur ses connaissances dans le domaine du génie électrique.

https://ladigitale.dev/digiview/#/v/684aaa5762af6

Attendez vous à voir vos certitudes voler en éclats !

Chapitre 1 - Définitions préalables

Découvrir le monde de l'électricité

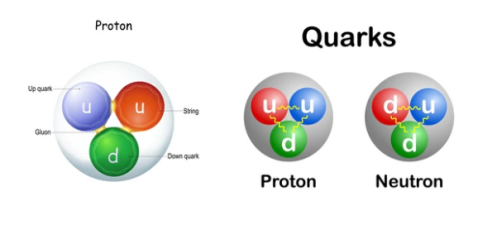
Petit détour par l'atome … L'électricité ou l'électronique n'est pas évidente à cerner. Le courant électrique ne se voit pas mais on peut observer ses effets. Ainsi souvent les élèves ont du mal à distinguer ce qu'est le courant électrique et la tension électrique. Tous se passe au niveau de l'atome. L'atome est en théorie la plus petite partie de matière pouvant se combiner avec un autre. L'on sait maintenant grâce aux accélérateurs de particules que le proton et le noyau sont constitués de particules plus élémentaires, les fermions qui renferment les quarks et les leptons.

Description

Les quarks et les leptons sont deux types de particules élémentaires qui constituent la matière selon le modèle standard de la physique des particules. Ils présentent plusieurs différences fondamentales.

Les quarks sont des particules qui interagissent via les trois forces fondamentales :

les interactions fortes,

les interactions électromagnétiques,

les interactions faibles.

Les leptons, en revanche, sont insensibles aux interactions fortes et ne forment pas de particules composites. Ils interagissent principalement via les interactions électromagnétiques et faibles.

Les leptons possèdent une charge électrique entière (soit -1, 0 ou +1) ou sont neutres, comme les neutrinos. Les leptons les plus connus sont l'électron, le muon, le tau et leurs neutrinos associés. Contrairement aux quarks, les leptons peuvent exister seuls dans la nature.

Les bosons sont des vecteurs qui permettent aux forces d'agir sur les particules. Ainsi en 2012 une expérience avec un accélérateur de particules a permis de prouver l'existence du boson de Higgs qui confère la masse aux particules.

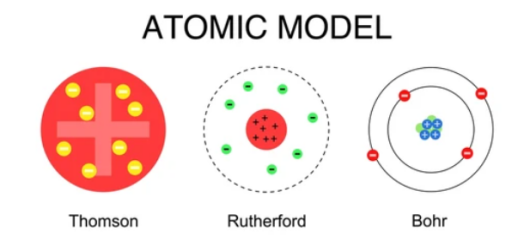
En physique, et également en sciences de l'ingénieur, on utilise des modèles pour décrire ce que nous observons expérimentalement. Ce dessous trois modèles sont proposés pour l'atome. Le modèle de Bohr est plus précis et permet d'observer que les électrons occupent des positions quantifiées autour de l'atome. Cela est en correspondance avec la mécanique quantique. Vous pouvez observer que dans un monde parfait l'atome est électriquement neutre, autant de charges positives que de charges négatives.

Comprendre l'électricité, c'est comprendre ce qu'il se passe à l'échelle atomique. A cette échelle de l'ordre de l'Ångström (10-10 m), les lois de la mécanique quantique sévissent et comme le disait Richard Feynman :

Si vous croyez comprendre la mécanique quantique, c’est que vous ne la comprenez pas.

Découvrir le courant électrique

Pourquoi des matériaux (notamment les métaux) conduisent-ils de l'électricité ?

Nous avons vu que l'atome selon le modèle de Bohr, proposait des électrons sur des orbites situées à une certaine distance du noyau . Pour être conducteur, l'atome doit libérer facilement des électrons libres. Les seuls candidats possibles sont les candidats de la dernière couche de l'atome. Prenons le cas d'un atome de cuivre, un très bon conducteur. Vous observerez qu'il ne dispose que d'un seul électron sur sa dernière couche. Ce dernier électron deviendra, suite à l'agitation thermique de l'atome, un électron libre. C'est cet électron libre qui pourra se déplacer et engendrer un courant électrique dans le matériau.

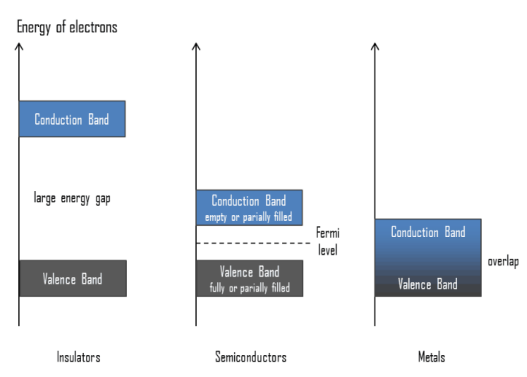
La figure ci-dessous montre l'énergie à apporter pour passer de la bande de valence (électrons associés à d'autres atomes par liaison covalente) à la bande de conduction. Vous observerez que pour les métaux ces deux bandes se chevauchent. Ce qui signifient que des électrons libres sont disponibles dans le matériau à 25 °C.

Remarque Pour les semi-conducteurs, le niveau de Fermi est une fonction de la température mais il peut être considéré, en première approximation, comme une constante, laquelle équivaudrait alors au niveau de plus haute énergie occupé par les électrons du système à la température de 0 K. Ce semi-conducteur pourra donc dans certaines circonstances devenir conducteur.

Pour les isolants, il faudra fournir une tension énorme pour les rendre conducteurs. Généralement cela provoque un arc et condamne le matériau. c'est également ce qui se passe lors d'un orage lorsque l'air devient conducteur. On dit alors que l'isolant claque.

Définition

Le courant électrique Le courant électrique sera défini comme le débit de charges circulant à l'intérieur du conducteur. On notera :

$I (Ampères)= {{\Delta Q (coulombs)} \over {\Delta t (secondes)}}$

Si on fait la limite de cette quantité on obtient :

$I = \lim\limits_{\Delta t \to 0} {{\Delta Q} \over {\Delta t}} = {{dQ} \over {dt}}$

Le saviez vous ? La charge d'un électron vaut 1,6×10−19 Coulombs.

Complément

Pour calculer le nombre d’électrons libres disponibles dans un fil de cuivre, on suit les étapes suivantes :

1. Données connues :

Section du fil : $S=2,5~mm^2$

Longueur : $L=10~cm=0,1~m$

Volume du fil : $V=S \times L=2,5 \cdot 10^{−6} \times 0,1=2,5 \cdot 10^{−7}~m^3$

Densité du cuivre : $\rho=8,96 \cdot 10^3 kg \cdot m^{-3}$

Masse molaire du cuivre : $M=63,5~g/mol=0,0635~kg/mol$

Constante d’Avogadro : $N_A=6,022 \cdot 10^{23}~atomes/mol$

Nombre d’électrons libres par atome de cuivre : 1 (le cuivre a 1 électron de conduction)

2. Calcul de la masse du fil :

$m=\rho \times V=8,96 \cdot 10^3×2,5 \cdot 10^{−7}=2,24 \cdot 10^{−3}~kg$

3. Nombre de moles de cuivre :

$n=m \times M=2,24 \cdot 10^{−3} \times 0,0635 \simeq 3,53 \cdot 10^{−2}~moles$

4. Nombre d’atomes de cuivre :

$N_{atomes}=n×N_A=3,53 \cdot 10^{−2} \times 6,022 \cdot 10^{23} \simeq 2,13 \cdot 10^{22}~atomes$

5. Nombre d’électrons libres :

Puisque chaque atome de cuivre fournit 1 électron libre :

$N_{électrons~libres}=N_{atomes} \simeq 2,13 \cdot 10^{22} ~\text{électrons}$

Fondamental

On remarque, que dans un conducteur il y a un nombre impressionnant d'électrons libres. C'est comme avoir un récipient fermé avec plein d'eau à l'intérieur. Comme une seringue remplie. Comment faire sortir ces électrons du conducteur ? Il faut exercer une « pression » électrique et cette « pression » se nommera la tension électrique. »

La force électrostatique

Remarque Faisons un peu de mécanique. Prenons une masse $m_1$ et une masse $m_1$ . Newton a montré que la force qui s'exerçait entre les deux masses était :

$F_{pes} = \frac{K \cdot m_1 \cdot m_2}{d^2}$

$F_{pes}$ : force de pesanteur en Newtons

$m_1$ : masse en kilos

$m_2$ : masse en kilos

$d$ : distance en mètres entre les deux masses

Si on pose le champ de pesanteur $G = \frac{K \cdot m_2}{d^2}$ il vient que $F_{pes} = m_1 \cdot G$

G représente ici le champ de pesanteur c'est à dire $9,81 m \cdot s^{-2}$ au niveau de la mer.

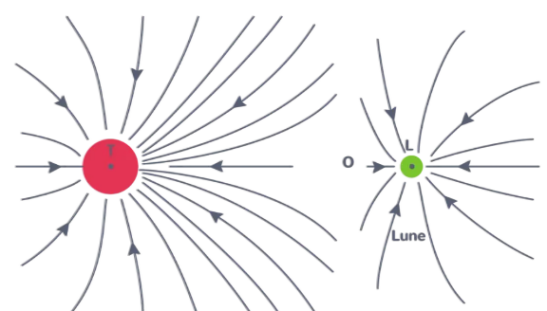
Le champ de pesanteur est représenté ci-dessous :

Cette illustration donne l'impression que la masse est déposée sur un drap et le déforme. En réalité elle déforme l'espace-temps.

Si l'on se place maintenant dans un contexte électrique avec deux charges on trouve une expression mathématique similaire :

$F_{pes} = \frac{K \cdot q_1 \cdot q_2}{d^2}$

avec :

$F_{elec}$ : force électrostatique en Newtons

$q_1$ : charge en coulombs

$q_2$ : charge en coulombs

d : distance en mètres entre les deux charges

Si on pose le champ électrique $E = \frac{K \cdot q_2}{d^2}$ il vient que $F_{pes} = q_1 \cdot E$ . Le champ électrique a pour unité des $V \cdot m^{-1}$ .

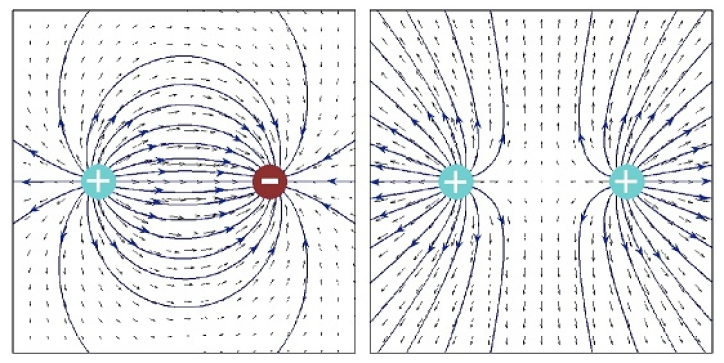
Le champ électrique est représenté ci-dessous :

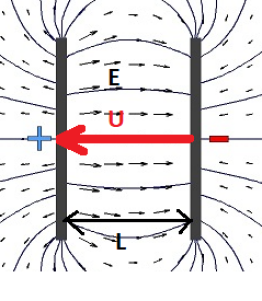
Si on place une charge positive sur une plaque et une charge négative sur une autre plaque on observe le champ suivant :

Remarque Les plus observateurs reconnaîtront ici la structure d'un condensateur. Notez également qu'entre deux plaques, le champ est quasi uniforme.

Attention

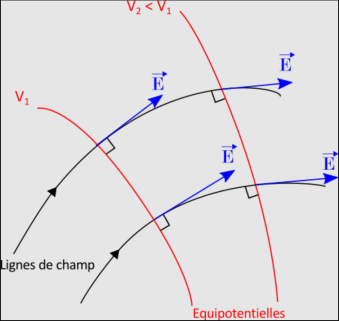
Mais ou se trouve la tension ?

Les équipotentielles sont des lignes qui relient les points ayant la même tension. Vous remarquerez que le champ se dirige d'un potentiel haut vers un potentiel bas. Ainsi la tension électrique correspond à une différence de potentiel électrique. Ceci signifie que sur le champ crée sur les deux plaques, les lignes de potentiel électriques correspondront à des lignes verticales entre les deux plaques. Ainsi une charge positive se trouve entre les deux plaques, elle sera accélérée par la force électrostatique. Elle se déplacera du potentiel le plus élevé (le plus chargé)(+) au potentiel le moins élevé (le moins chargé)(-).

Ainsi, dans un champ uniforme on peut noter : $U = E \cdot d$

avec :

U: différence de potentiel électrique ou tension en Volts

E: champ électrique en $V \cdot m^{-1}$

d: distance en mètres

Remarque

Calculons le travail de la force électrique entre les plaques :

$W(F_{elec}) = F_{elec} \cdot d = q \cdot E \cdot d$

$~soit~ W(F_{elec})= q \cdot U$

$~comme ~q = I \cdot t$

$~ W(F_{elec})= (U \cdot I) \cdot t$

$~ W(F_{elec})= P_{elec} \cdot t$

avec :

$W(F_{elec})$ : travail en joules

U : tension en volts

I : intensité du courant en ampères

$P_{elec}$ : puissance électrique en watts

Pour le champ de pesanteur le travail serait :

$W(F_{pes}) = F_{pes} \cdot h= m \cdot g \cdot h$

$soit~ W(F_{pes})= (F_{pes} \cdot v) \cdot t$

$W(F_{pes})= P_{meca} \cdot t$

avec :

$W(F_{pes})$ : travail en joules
$F_{pes}$ : force en Newtons
$v: vitesse~en~m \cdot s^{-1}$
$P_{meca}$ : puissance mécanique en watts

La puissance est toujours le produit de deux grandeurs : une grandeur effort et une grandeur flux.

Puissance	Grandeur effort	Grandeur flux	Formule
Électrique	Tension	Courant	$P = U \cdot I$
Mécanique Translation	Force	Vitesse	$P = F \cdot v$
Mécanique Rotation	Couple	Vitesse angulaire	$P = C \cdot \Omega$
Hydraulique	Pression	Débit	$P = p \cdot Q$

Définition

Comme $W=Q \cdot U$ on en déduit que $U = \frac{W}{Q}$ . La tension correspond donc à l'énergie nécessaire pour déplacer une charge d'1 coulomb.

Complément

Nous avons ainsi montré que le domaine mécanique avait son entité élémentaire : la masse. Dans le domaine électrique il s'agit de la quantité d'électricité. On retrouve le même formalisme mathématique pour les deux domaines. Les lois de conservations de masse et de la quantité d'électricité sont deux lois fondamentales en physique.

Finalement tout se joue à l'échelle de l'atome : le boson de Higgs confère une masse particules, et il se trouve au sein de l'atome des particules possédant une charge électrique. Le monde de l'électricité n'est finalement pas si éloigné que cela du monde de la mécanique. En électricité tout comme en mécanique les explications se situent bien souvent à l'échelle atomique !