Association de résistances
Résistances en série
Deux résistances sont placées en série. Par quelle résistance faut-il les remplacer pour obtenir une résistance équivalente ?
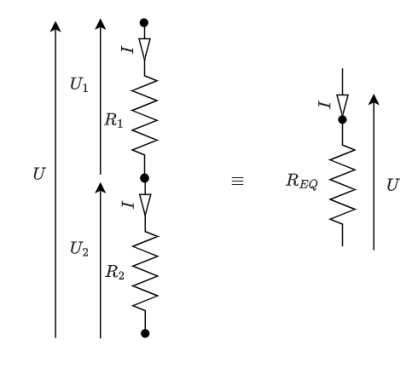
La loi d'ohm sur\( R_1\) permet d'écrire : \(U_1 = R_1 \cdot I\) .
La loi d'ohm sur \(R_2\) permet d'écrire :\( U_2 = R_2 \cdot I\) .
La loi d'ohm sur \(R_{EQ}\) permet d'écrire :\( U = R_{EQ} \cdot I\) .\(\newline\)
On remarque également que \(U = U_1+ U_2\) soit \(U = R_1 \cdot I + R_2 \cdot I = (R_1 + R_2) \cdot I\).\( \newline\)
\(\left\{\begin{eqnarray} U & = & R_{EQ} \cdot I \\ U & =& (R_1 + R_2) \cdot I \end{eqnarray}\right . \newline\)
Conclusion \(\boxed{R_{EQ}=R_1 + R_2} \newline\)
Définition :
La résistance équivalente à plusieurs résistances en série vaut la somme de ces résistances.
Dans ce contexte on doit parler du pont diviseur de tension qui est un circuit constitué d 'au moins deux résistances en série. Quelle est la relation entre \(U\),\( U_2\), \(R_1\) et \(R_2\) ?
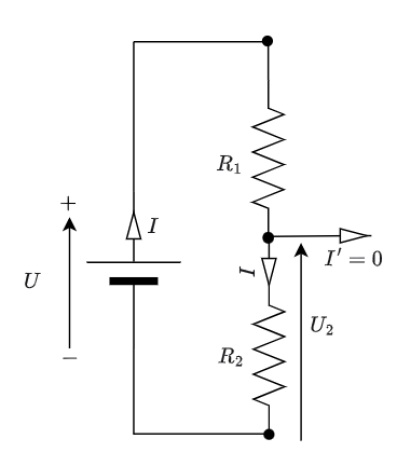
La loi d'ohm sur \(R_2\) permet d'écrire :\(~U_2 = R_2 \cdot I\) .
La loi d'ohm sur \(R_{EQ}\) permet d'écrire :\(~U = R_{EQ} \cdot I = (R_{1} + R{2}) \cdot I\).
\(~I = {\frac {U}{R_1+R_2}}\)
On déduit que :\(~ U_2 = R_2 \cdot {\frac {U}{R_1+R_2}}\) soit \(~ \boxed{U_2 =U\cdot {\frac {R_2}{R_1+R_2}}}\)
Résistances en dérivation
Deux résistances sont placées en dérivation. Par quelle résistance faut-il les remplacer pour obtenir une résistance équivalente ?
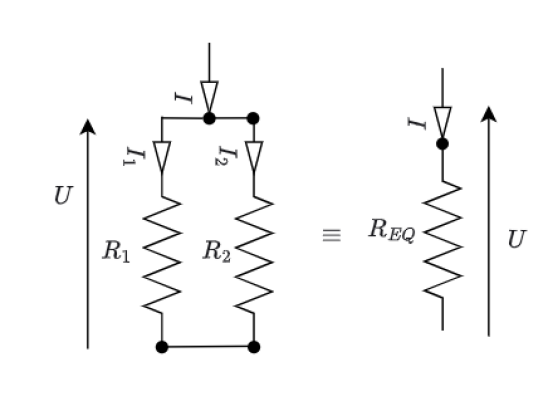
La loi des nœuds permet d'écrire : \(I = I_1+ I_2\)
La loi d'ohm sur\( R_1\) permet d'écrire : \(I_1 = U \div R_1\) .
La loi d'ohm sur \(R_2\) permet d'écrire :\( I_2 = U \div R_2\) .
La loi d'ohm sur \(R_{EQ}\) permet d'écrire :\(I = U \div R_{EQ}\) .\(\newline\)
\(\boxed{\frac{1}{R_{EQ}} = \frac{1}{R_{1}} +\frac{1}{R_{2}}} \newline\)
Conclusion \(\boxed{R_{EQ}=\frac{R_1 \cdot R_2}{R_1+R_2}}\newline\)
Définition :
L'inverse de la résistance équivalente à plusieurs résistances en dérivation vaut la somme de l'inverse de ces résistances.
Remarque :
Deux résistances en dérivation se comporte comme un diviseur de courant. \(\newline\)
Notons \(U = R_1 \cdot\) \(I_1 = R_eq \cdot I\) . Soit\(~I_1 = {\frac {R_{EQ}} {R_1}} \cdot I = {\frac {\frac{R_1 \cdot R_2}{R_1+R_2}} {R_1}} \cdot I \newline\).
\(\boxed{I_1 = {\frac {R_{2}} {R_1+R_2}} \cdot I}\) \(~\boxed{I_2 = {\frac {R_{1}} {R_1+R_2}} \cdot I} \newline\)
En posons \(G_1 = 1 \div R_1\) et \(G_2 = 1 \div R_2\) on arrive à \(\boxed{I_1 = {\frac {G_{1}} {G_1+G_2}} \cdot I}\) \(~\boxed{I_2 = {\frac {G_{2}} {G_1+G_2}} \cdot I} \newline\)