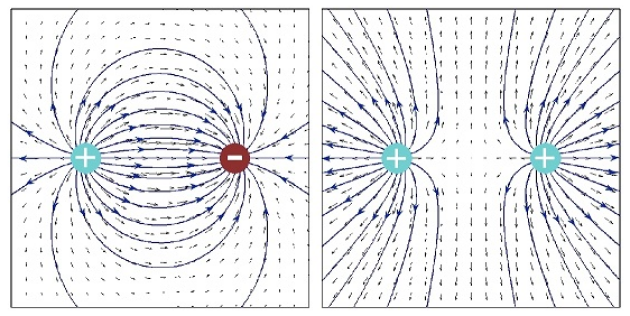
La force électrostatique
Remarque :
Faisons un peu de mécanique. Prenons une masse m1 et une masse m2. Newton a montré que la force qui s'exerçait entre les deux masses était :
\(\newline\)
\(F_{pes} = G \cdot {{m_1 \cdot m_2} \over d^2}\)
\(F_{pes} : \) : force de pesanteur en Newtons
\(m_1\): masse en kilos
\(m_2\): masse en kilos
\(d\) : distance en mètres entre les deux masses
\(\newline\)
Si on pose le champ de pesanteur \(g = G \cdot {{m_2} \over d^2}\) il vient que \(F_{pes} = m_1 \cdot g\)
\(\newline\)
g représente ici le champ de pesanteur c'est à dire 9,81 m\( \cdot \)s-2 au niveau de la mer.
\(\newline\)
Le champ de pesanteur est représenté ci-dessous :
\(\newline\)
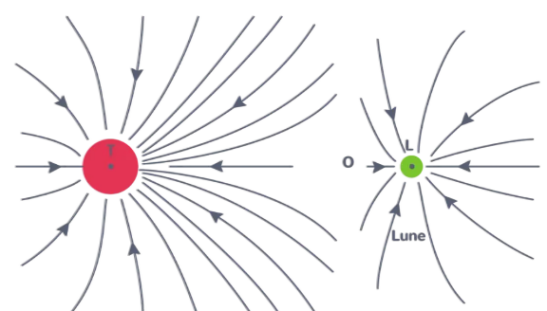
Ce schéma donne l'impression que la masse est déposée sur un drap et le déforme. En réalité elle déforme l'espace-temps.
Si l'on se place maintenant dans un contexte électrique avec deux charges on trouve une expression mathématique similaire : \(\newline\)
\(F_{électro} = k \cdot {{q_1 \cdot q_2} \over d^2} \newline\) avec : \(\newline\)
\(F_{électro} : \) : force électrostatique en Newtons
\(q_1\) : charge en coulombs
\(q_2\) : charge en coulombs
\(d\) : distance en mètres entre les deux charges
\(\newline\)
Si on pose le champ électrique \(E = k \cdot {{q_2} \over d^2}\) il vient que \(F_{électro} = q_1 \cdot E\). Le champ électrique a pour unité des volts\( \cdot\) m-1.
\(\newline\)
Le champ électrique est représenté ci-dessous : \(\newline\)
Si on place une charge positive sur une plaque et une charge négative sur une autre plaque on observe le champ suivant : \(\newline\)
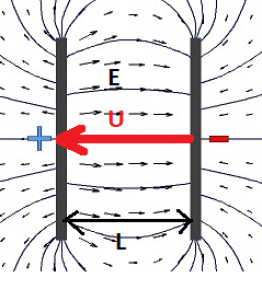
Remarque :
Les plus observateurs reconnaîtront ici la structure d'un condensateur. Notez également qu'entre deux plaques, le champ est quasi uniforme. \(\newline\)
Attention :
Mais ou se trouve la tension ?
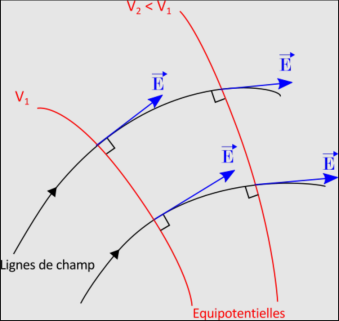
Les équipotentielles sont des lignes qui relient les points ayant la même tension. Vous remarquerez que le champ se dirige d'un potentiel haut vers un potentiel bas. Ainsi la tension électrique correspond à une différence de potentiel électrique. Ceci signifie que sur le champ crée sur les deux plaques, les lignes de potentiel électriques correspondront à des lignes verticales entre les deux plaques. Ainsi une charge positive se trouve entre les deux plaques, elle sera accélérée par la force électrostatique. Elle se déplacera du potentiel le plus élevé (le plus chargé)(+) au potentiel le moins élevé (le moins chargé)(-). \(\newline\)
Ainsi, dans un champ uniforme on peut noter : \(\newline\)
\(U = E \cdot L\) \(\newline\)
avec : \(\newline\)
\(U\) : différence de potentiel électrique ou tension en Volts
\(E \): champ électrique en Volts \(\cdot\) m-1
\(L\) : distance en mètres
\(\newline\)
Remarque :
Calculons le travail de la force électrique entre les plaques :\( \newline\)
\(W(F_{elec}) = F_{elec} \cdot L = q \cdot E \cdot L \newline soit~ W(F_{elec})= q \cdot U \newline comme ~q = I \cdot t \newline W(F_{elec})= (U \cdot I) \cdot t \newline W(F_{elec})= P_{elec} \cdot t\)
avec : \(\newline\)
\(W(F_{elec}) \): travail en joules
\(U\) : tension en volts
\(I \): intensité du courant en ampères
\(P_{elec}\) : puissance électrique en watts
\(\newline\)
Pour le champ de pesanteur le travail serait :\( \newline\)
\(W(F_{pes}) = F_{pes} \cdot h= m \cdot g \cdot h \newline soit~ W(F_{pes})= (F_{pes} \cdot v) \cdot t \newline W(F_{pes})= P_{meca} \cdot t\)
avec : \(\newline\)
\(W(F_{pes}) \): travail en joules
\(F_{pes}\) : force en Newtons
\(v\): vitesse en m\( \cdot \)s-1
\(P_{meca}\) : puissance mécanique en watts
\(\newline\)
La puissance est toujours le produit de deux grandeurs : une grandeur effort et une grandeur flux.
Puissance | Grandeur effort | Grandeur flux | Formule |
|---|---|---|---|
Electrique | Tension | Courant | \(P = U \cdot I\) |
Mécanique Translation | Force | Vitesse | \(P = F\cdot v\) |
Mécanique Rotation | Couple | Vitesse angulaire | \(P = C\cdot \Omega\) |
Hydraulique | Pression | Débit | \(P = p\cdot Q\) |
Définition :
Comme \(W=Q \cdot U\) on en déduit que \(U = W/Q \). La tension correspond donc à l'énergie nécessaire pour déplacer une charge d'1 coulomb.\( \newline\)
Complément :
Nous avons ainsi montré que le domaine mécanique avait son entité élémentaire : la masse. Dans le domaine électrique il s'agit de la quantité d'électricité. On retrouve le même formalisme mathématique pour les deux domaines. Les lois de conservations de masse et de la quantité d'électricité sont deux lois fondamentales en physique.\(\newline\)
Finalement tout se joue à l'échelle de l'atome : le boson de Higgs confère une masse particules, et il se trouve au sein de l'atome des particules possédant une charge électrique. Le monde de l'électricité n'est finalement pas si éloigné que cela du monde de la mécanique. En électricité tout comme en mécanique les explications se situent bien souvent à l'échelle atomique ! \(\newline\)