Théorème de superposition
Théorème de superposition
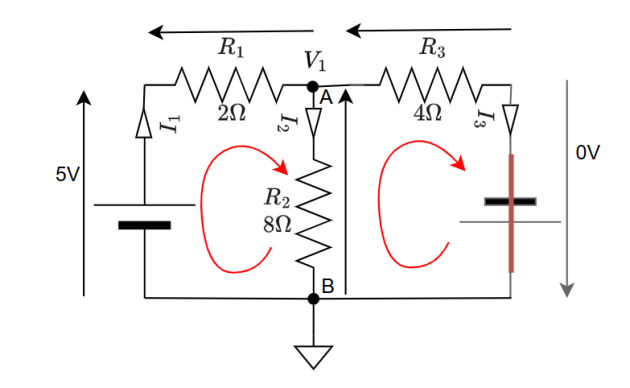
Quand un réseau linéaire comporte plusieurs générateurs, l' intensité du courant dans une branche de ce réseau est égale à la somme (algébrique) des intensités des courants créés par chacun des générateurs dans cette branche, les autres générateurs étant remplacés par leur résistance interne ou un court circuit pour un générateur parfait .\( \newline\)
On court-circuite le second générateur. Déterminons \(I_1', I_2' ~et~ I_3'\). La résistance de 4 ohms se retrouve en dérivation de la résistance de 8 ohms. La loi d'ohm permet d'écrire :
\(V_1 = R_8 \cdot I_2'\)
\(V_1 = R_4 \cdot I_3'\)
\(\newline\) Si on considère une résistance équivalente entre A et B, la loi d'ohm permettrait d'écrire \(V_1 = R_{AB} \cdot I_1'\). \(\newline\)
La loi des nœuds en A permet d'écrire \(I_1' = I_2'+ I_3'\). Donc \(\frac {V_1}{R_{AB}} =\frac {V_1}{R_{8}}+\frac {V_1}{R_{4}}\) soit \(\frac {1}{R_{AB}} =\frac {1}{R_{8}}+\frac {1}{R_{4}} \text{ soit } \boxed{R_{AB} = {\frac{R_4 \cdot R_8}{R_4 +R_8}}} \text{ soit } 2.66 ~\Omega \newline\) . Donc \(I_1' = {\frac {5} {2+2.66} } = 1,0714 A \).
\(V_1' = 5 - 2 \cdot 1,0714 = 2.857 V. I_2' = {\frac {2.857} {8} } = 0,357 A \text{ et }I_3' = {\frac {2.857} {4} } = 0,714 A\).\( \newline\)
\(\boxed{I_1' = 1.0714\ \text{A},\quad I_2' = 0.357\ \text{A},\quad I_3' = 0.714\ \text{A}}\) .
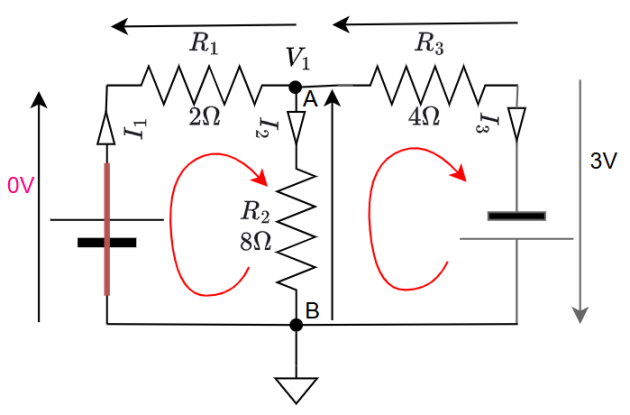
On court-circuite le premier générateur. Déterminons \(I_1", I_2" ~et~ I_3"\). La résistance de 2ohms se retrouve en dérivation de la résistance de 8 ohms. La loi d'ohm permet d'écrire :
\(V_1 = R_8 \cdot I_2"\)
\(V_1 = R_2 \cdot I_3"\)
\(\newline\) Si on considère une résistance équivalente entre A et B, la loi d'ohm permettrait d'écrire \(V_1 = R_{AB} \cdot I_1"\). \(\newline\)
La loi des nœuds en A permet d'écrire \(I_1" = I_2"+ I_3"\). Donc \(\frac {V_1}{R_{AB}} =\frac {V_1}{R_{8}}+\frac {V_1}{R_{2}}\) soit \(\frac {1}{R_{AB}} =\frac {1}{R_{8}}+\frac {1}{R_{2}} \text{ soit } \boxed{R_{AB} = {\frac{R_2 \cdot R_8}{R_2 +R_8}}} \text{ soit } 1.6 ~\Omega \newline\) . Donc \(I_3" = {\frac {3} {4+1.6} } = 0,5357 A \).
\(V_1" = -3+ 4 \cdot 0.5357= -0,8571 V\text{. } I_2" = {\frac {0,8571} {8} } = 0,10714 A \text{ et }I_1" = {\frac {0,8571} {2} } = 0,42857 A\).\( \newline\)
\(\boxed{I_1" = 0,42857\ \text{A},\quad I_2" = 0,10714\ \text{A},\quad I_3" = 0,5357 A\ \text{A}}\) . \(\newline\)
En additionnant la superposition des deux tensions on obtient \(V_1 = 2.857 - 0.857 = 2 V\) ce qui est cohérent.
\(\newline\) Attention : ici le générateur envoie le courant par le bas. L'équation est donc en B.\(~ I_3"\) est positif,\(~I_1"\) et \(~I_2"\) sont négatifs. En A\(~I_1"\) et \(~I_2"\) sont positifs mais\(~I_3"\) est négatif. Finalement\(~I_1'\) et\(~I_1"\) sont dans le même sens. \(~I_3' \)et\(~I_3"\) également. Seuls\(~I_2'\) et\(~I_2"\) s'opposent.
En additionnant la superposition des deux courants on obtient \(\boxed{I_1 = 0,42857+1.0714\ \text{A},\quad I_2 = 0.357-0,10714\ \text{A},\quad I_3 = 0,5357+0.714\ \text{A}}\) . \(\boxed{I_1 = 1.5\ \text{A},\quad I_2 = 0.25\ \text{A},\quad I_3 = 1.25\ \text{A}}\)
\(\newline\)